BaseCaseNotNeeded

DRAFT

Not Observed

Correction

Here is what's right.

Any terminating recursive computation needs some kind of base case.

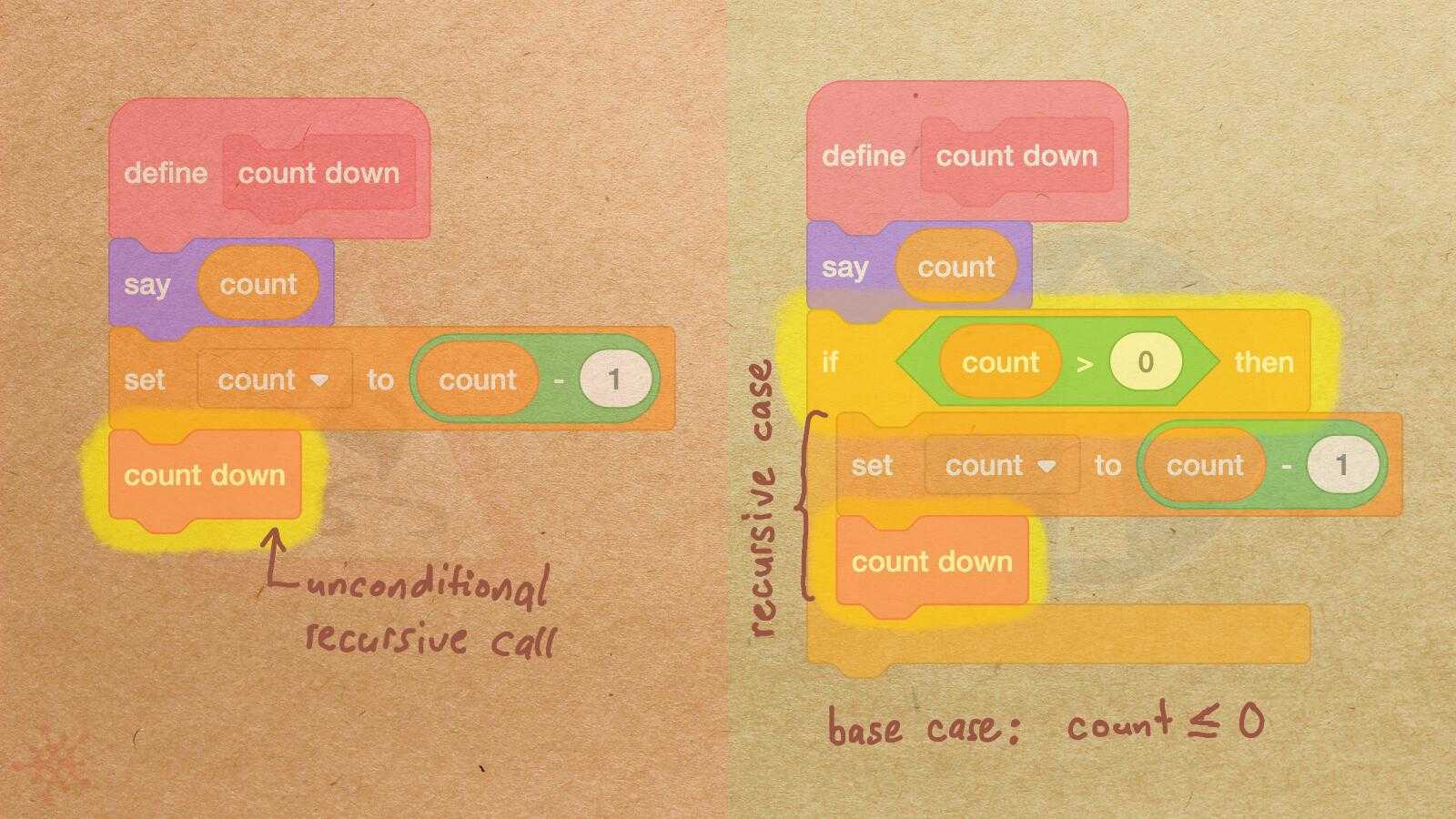
The following directly-recursive custom block wihout base case represents a recursive computation that will not terminate:

The following custom block does have a base case:

For a recursive computation to terminate there needs to be some base case. In the above example, the base case is when the condition of the if-then block evaluates to false, and thus the recursive call is skipped.

Origin

Where could this misconception come from?

Value

How can you build on this misconception?

Base Cases in Indirect Recursion

If a student has this misconception, it may be good to point out that in cases of indirect recursion, where several custom blocks are involved in a recursive cycle, it is sufficient if one of them takes care of the base case. The other custom blocks involved in the recursive cycle thus might not contain any code to deal with terminating the recursion.

Very Advanced: Recursion Without Base Case with Lazyness

Lazy languages (like Haskell) can have recursive functions without base cases and still have computations that terminate. For example, the function from in the following Haskell code is recursive, but it has no base case. In an eager language, any call of from would generate an infinitely long list. In Haskell, which is lazy, the call is not evaluated until it is needed. Thus, take 5 (from 0) will only lead to the first 5 elements of the infinitely long sequence being created, i.e., the first five invocations of from to be evaluated.

from n = n:(from (n+1))
take 5 (from 0)